排序算法——冒泡排序

冒泡排序

大部分人学习排序的第一个算法，就是冒泡排序。

简单来说，冒泡排序就是每次迭代，都会检查相邻的 2 个元素大小，如果左边比右边大，就交换顺序（升序），这样，第一轮下来，一定会把最大的那个值放到最右边。到第二轮的时候，也同样会把未排序的最大的数字，放到倒数第二的位置……..

第一轮排序，如下图：

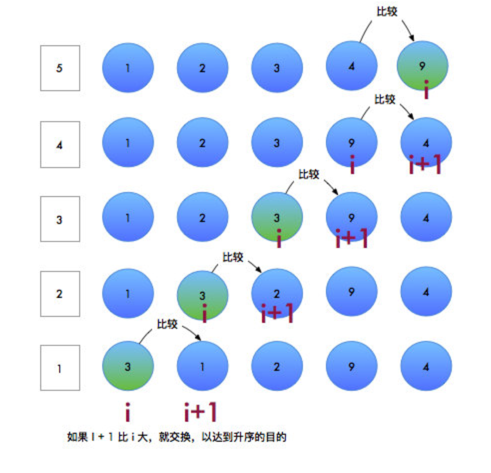
解释一下上图，左边是排序次数，一共 5 次。

从最下面开始冒泡，i 从 0 开始，每次比较 i 和 i + 1 的大小，如果 i 大，就把他俩进行交换，例如第一次比较中， i 比 i + 1 大，所以，在第二行，进行了交换。 同时，i 进行自增，继续重复上个过程。知道将最大的元素 9 放到最后一个格子，从而完成一轮排序。

简单说，冒泡排序，每次都会找到最大的数字，然后将其放到最后的位置进行排序。

代码如下：

public static void sort升序(int[] arr, int n) {
        for (int i = 0; i < arr.length; i++) {
            for (int j = 0; j < arr.length - 1; j++) {
                if (arr[j] > arr[j + 1]) {
                    int tmp = arr[j + 1];
                    arr[j + 1] = arr[j];
                    arr[j] = tmp;
                }
            }
        }
}

上面的代码中，我们使用 2 层循环，最内层循环比较 j 和 j + 1 的大小。从而实现上面的思路。

那么，代码还有优化空间吗？

答案是有的。

我们使用这样一组数据，进行排序：

int[] arr = {5, 1, 11, 2, 0, 6, 9, 4 };

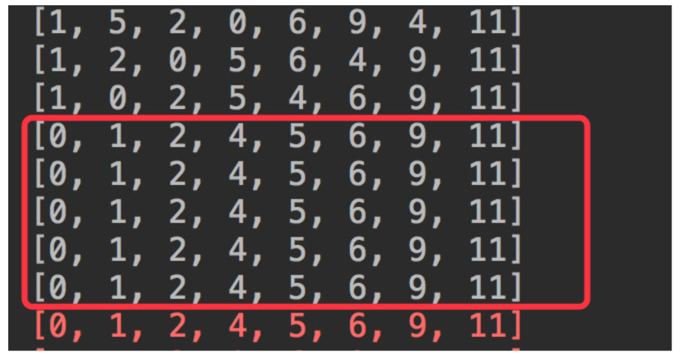
可以看到，该数组基本有序。我们打印每次循环之后的数组的值，发现只要 4 次，就已经完成排序，后面的实际上就不需要继续执行了。

所以，如果进行优化的话，只要内部没发生调换事件，实际数组就是有序的了，就可以直接结束排序算法。

还可以继续优化吗？

我们的代码中，内循环条件每次都是 i < arr.length. 需要吗？

答案是不需要。

因为，每次我们都能找到“未排序”分区中，最大的那个数字，并将其放到最右边正确的位置，所以，当每次冒泡结束，下次再循环时，最后面的那个格子，就不用再次进行比较了——因为他的位置已经是正确的。

所以，内层 for 循环的表达式，应该是 j < arr.length - i - 1;

结合两个优化，代码如下：

public static void sort升序(int[] arr, int n) {
    for (int i = 0; i < arr.length; i++) {
        boolean flag = false;
        for (int j = 0; j < arr.length - 1 - i; j++) {
            if (arr[j] > arr[j + 1]) {
                int tmp = arr[j + 1];
                arr[j + 1] = arr[j];
                arr[j] = tmp;
                flag = true;
            }
        }
        if (!flag) {
            break;
        }
        System.out.println(Arrays.toString(arr));
    }
}

1. 使用 flag 控制是否还需要继续循环，例如当原始数据源本身就是升序的，那么，就可以在很少的冒泡次数下，完成排序，当有一次没有发生交换数据事件，表明排序已经完成，应当结束排序。
2. 使用 j < arr.length - 1 - i 进行优化，因为每次循环后，倒数第 i 个格子的数据，肯定是正确的，不需要再次进行比较，因此，可以过滤这个格子以及后面的格子。

日常三问

1. 冒泡排序是原地排序算法吗？

答案是的；冒泡排序在进行比较以及交换的操作中，并没有使用其他空间，空间复杂度是 1， 因此是一个原地排序算法。

2 冒泡排序是稳定的排序算法吗？

答案：看你的实现。

如果我们的比较是 if（arr[j] > arr[j+1]）这么写的，那么就是稳定的，因为相等的两个数字，并没有进行交换，但是，如果加上了 = 号，就不是稳定的。

2. 冒泡排序的时间复杂度是多少？

时间复杂度， 3 个角度：最好，最差，平均。

最好，数据本身就是有序的，只要一遍，就能知道其是有序的，复杂度是 N。

最差，数据是逆序的，需要 n * n 次操作，复杂度是 n^2.

平均，之前我们知道，可以用概率论的方式，来进行平均时间复杂度的计算。还有另一种方式，就是“有序度”和“逆序度”这两个概念进行分析。

有序度和逆序读

有序度是数组中具有有序关系的元素对的个数。

例如数组 : {5, 1, 11, 2, 0, 6, 9, 4 }，具有“有序关系” 的元素有：

可以看到，有 15 对数据是有序的。公式为arr[i] <= arr[j] && i < j​.

那如果整个数组都是有序的，那有多少有序元素呢？

假设 5 个元素：$「1，2，3，4，5」$

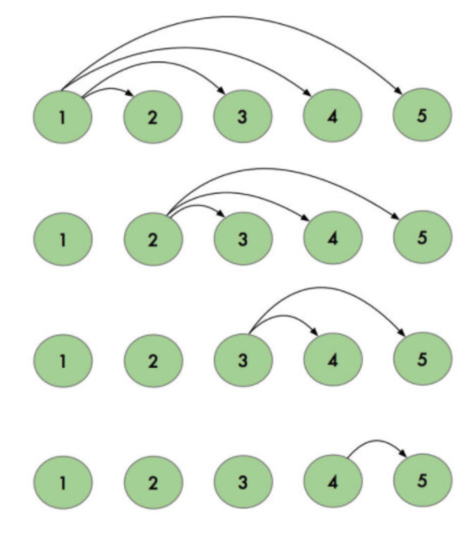
有以上组合，公式为 n(n - 1) / 2.

数组 {5, 1, 11, 2, 0, 6, 9, 4 } 有 8 个元素，满有序度为 38 ，而实际有序度为 15，那么逆有序度为 38 - 15 = 17. 本质上，我们排序的过程，就是将逆有序的元素，变成有序的元素。即增加有序度，减少逆序度。

在最好情况下，有序度为 n*(n-1)/2，我们不需要任何操作。

在最好情况下，有序度为 0。我们要进行 n*(n-1)/2 次交换。

如果使用这种方式计算“平均时间复杂度”？

我们可以取一个数据有序度 不是很高，也不是很低的，例如 $n *\frac{ (n-1)} {4}$，来当做平均时间复杂度，可以看到，去去除低阶和系数，复杂度还是 $O(n^2)$，注意，这里只是交换操作，还有比较操作没算进去，因此，冒泡排序的时间复杂度就是 $O(n^2)$.

虽然这种方式不是很严格—— 相对于使用概率论。但很多时候还是挺实用的。（大话数据结构中，也是这么计算平均时间复杂度的。但如果要真正的计算的比较准确，需要对数据规律进行统计，然后使用概率进行计算）

EOF