快速排序

简述

快排是排序算法中绕不开的关键一环，其中涉及到分治算法，二分查找等关键知识。

本文内容：

1. 快排原理
2. 代码实现
3. 分区过程图示
4. <啊哈算法> 中的另一种实现
5. 复杂度
6. 优化

快排原理

快排也归并类似，也使用了分治的思想，即将原序列划分成 2 份，然后继续递归。但是他们的区别是：

归并的划分是简单的通过找中位下标进行，他的公式是 $mid = \frac {(low + high)}2$
快排的划分，是通过一个参考值，将每个数据和参考值比较，然后将划分成 2 份，左边的比参考值小，右边的比参考值大。他的公式是 ：$mid = partitin(A, low, high)$ ，通过一个 partition 函数，找到一个 mid 值。

在算法导论中，伪代码是这样的：

代码中，先使用 partition 函数，获取 mid 值，然后，将 2 个序列继续进行递归调用。

其中，partition 的关键函数如下：

算法会设计两个指针 i 和 j，i 左边的数据表示已经排好序的元素，j 指针用来寻找比 参考值 x 小的 元素。如果 j 所在的元素比 x 小，就将 i 和 j 交换，并将 i 指针前进一步。最后，将 i 所在的元素和 x 进行互换，达到分区的目的。

代码实现

static void quickSort(int[] arr, int low, int high) {
     if (low >= high) {
         return;
     }
     int mid = partition(arr, low, high);
     quickSort(arr, low, mid - 1);
     quickSort(arr, mid + 1, high);
 }

 static int partition(int[] arr, int low, int high) {

     int x = arr[high];
     int i = low;
     int j = low;

     while (j < high) {
         if (arr[j] <= x) {
             swap(arr, i++, j);
         }
         j++;
     }

     swap(arr, i, high);

     return I;
 }

 static void swap(int[] arr, int low, int high) {
     int tmp = arr[low];
     arr[low] = arr[high];
     arr[high] = tmp;
 }

上面的代码中，关键就是 parttion 函数，我们使用了 i 和 j 两个指针，每次 j 都会自增，如果 j 比 x 小，那么，就将 j 和 i 交换，同时 i 自增。目的就是让 i 左边的序列是有序的，j 和 i 之间不会存在比 x 小的元素。j 的作用是寻找比 x 下的元素，直到 j == hight。

图示

假设我们现在有一个序列：

{2, 3, 1, 6, 9, 0 ,4, 8, 5}

排序过程是怎么样的呢？

首先，参考值 x 是 5.

我们从最左边开始，和 x 比较。

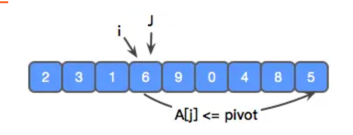
左边的 2，3，1 元素，都比 5 小，直接跳过，i 和 j 指针同时进行。直到遇到 6 ，比 x 大，此时，i 停止，保证 i 左边的元素是有序的，j 继续寻找 比 x 小的元素。

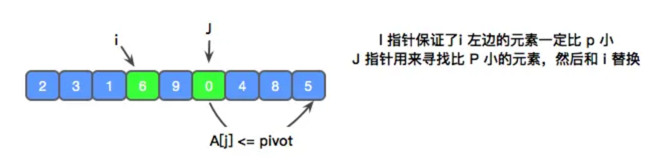
j 找到了 0 这个元素，比 x 小，此时 i 还在 6 这个位置，因此，我们可以将 i 和 j 进行交换，并将 i 前进一位，使 i 左边的序列继续有序。j 继续向前扫描。

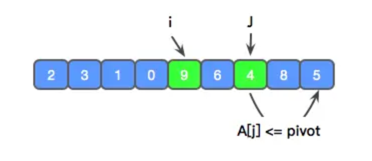
j 又找到了 4 个元素，比 x 小，算法重复上个步骤：将 i 和 j 交换，i 和 j 都前进一步。

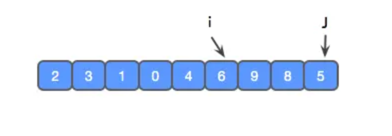
现在 j 走到了尽头，此时我们需要将参考值 x 和 i 进行交换，使 x 左边比 x 小，x 右边 比 x 大，并返回 x 所在的下标。

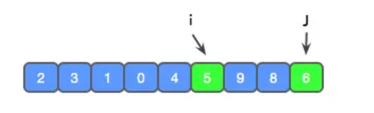
此时，完成了一次分区。

<啊哈算法> 中的另一种实现

在另一本算法普及书《啊哈算法》 中，也实现另一个快排，不过，和算法导论的有一点点区别，区别在于指针的开始阶段不同。

算法导论的指针，i 和 j 是从同一个方向开始的。
啊哈算法中的指针，i 总左边开始，j 从右边开始，两个指针相遇，就停止循环。

在我的电脑中进行测试，后者的性能，要比前者更好。

我们看看后者的分区过程是怎么样的。

现在我们有一个无序数组：

{2, 3, 1,6, 9, 0,4,8,5}

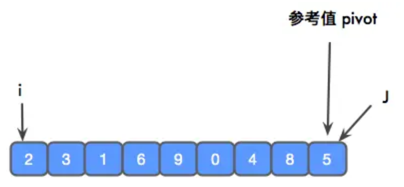
首先，参考值是 5，i 从左边开始，j 从右边开始，i 用于寻找比 pivot 大的元素，j 用于寻找比 pivot 小的元素，然后将 i 和 j 进行交换。

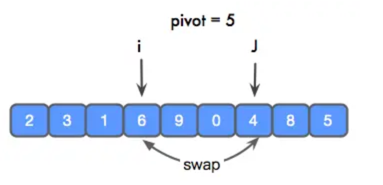
上图中，i 为了找到 比 pivot 大的元素，走到了 6 的位置，j 为了找到比 pivot 小的元素，走到了 4 的位置，然后进行交换。然后，各自继续前进。

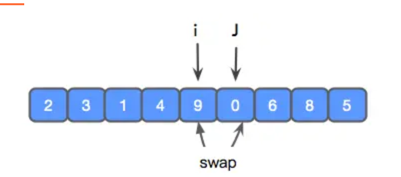
重复上次的操作，进行交换，并前进一步。

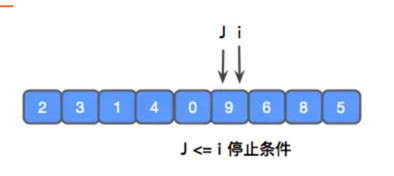
此时，i 和 j 相遇，停止循环，此时，需要将 pivot 和 i 进行交换，让 pivot 左边的比自身小，pivot 右边的，比自身大。

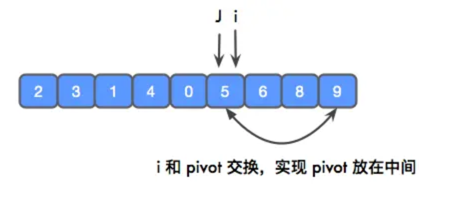
此时，完成了一次分区。

代码实现如下：

public static void qSort(int[] arr, int head, int tail) {
    if (head >= tail || arr == null || arr.length <= 1) {
        return;
    }
    int i = head, j = tail, pivot = arr[tail - 1];
    while (i <= j) {
        while (arr[i] < pivot) {
            ++i;
        }
        while (arr[j] > pivot) {
            --j;
        }
        if (i < j) {
            int t = arr[i];
            arr[i] = arr[j];
            arr[j] = t;
            ++i;
            --j;
        } else if (i == j) {
            ++i;
        }
    }
    qSort(arr, head, j);
    qSort(arr, i, tail);
}

我在我的电脑上，使用如下数据进行测试：

public static void main(String[] args) {
    long s = System.currentTimeMillis();
    int[] arr = new int[10000000];

    for (int i = 0; i < 10000000; i++) {
        arr[i] = ThreadLocalRandom.current().nextInt(90000);
    }

    qSort(arr, 0, arr.length - 1);

    long e = System.currentTimeMillis();

    System.out.println("time : " + (e - s));
}

1k 万的数据，使用首尾指针，时间是 800ms 左右，使用前后指针，时间是 1100ms 左右。（归并的排序时间是 1300ms）。

个人认为，差距在于：前后指针，如果数据是的有序度是50%，那么 i 和 j 的指针会走 150% 次，而首尾指针则只会走100% 次。这个是常量级的时间损耗。

复杂度

快排和归并一样，使用分治算法，但是他们时间复杂度并一样：
最好：$O(nlogn)$
最坏：$O(n^2)$
平均：$O(nlogn)$

空间复杂度，注意，虽然快排是原地排序，但是由于使用递归，递归本身就是栈，因此，递归的深度就是他的空间复杂度，而递归的深度就是 $O(logn)$，因此，他的空间复杂就是 $O(logn)$，不是 $O(1)$.

快排是稳定的排序算法吗？

答案：不是。

假设现在有一个序列：$6，8，7，6，3，5，9，4$

我们以 4 作为 pivot ，在第一次分区，进行交换后，6 和 3 的位置进行交换，此时， 两个 6 的位置就变化了，因此，快排不是稳定的排序算法。

优化

快排的优化，在于如何选取合适 的 pivot 。

为什么这么说。

如果快排的原始数据是接近有序的，那么，分区函数的性能将急剧下降，退化成 $O(n^2)$.

为什么？试想，我们每次选取的 pivot 都是最后一位，分区函数如果想找到正确的分区点，需要交换整个序列。如果想递归完成所有分区操作，则需要 n 次，而不是 logn 次。

而最好的状态就是，分区之后，两边的数据量是均等的。

那么，如何取 pivot 就很重要了。

通常有 2 种方式：

1. 随机数，从概率上来说，随机数，能够保证命中的概率是一致的。
2. 3 个数字取中法。我们从首、尾、中，三个地方取出数字，取其中间值当做 pivot。如果数量量比较大，就需要 5 数取中，10 数取中等方法。

另外，由于快排是使用递归的，因此，如果递归栈过深，可能导致堆栈溢出，因此，如果堆栈很深，可以手动模拟堆栈实现。防止堆栈溢出。归并也是同样的道理。

总结

快排的思想很优秀，使用了分治思想，原地排序。

但是他也有缺点。

1. 不是稳定的排序算法
2. 如果数据本身有序度很高，那么，算法性能将急剧退化，需要使用优化策略处理。

关于优化，很多排序函数不会仅仅只用一种算法。

例如：

在数据量很小的时候，使用归并排序，因为算法稳定，$O（n）$的空间复杂度问题也不大。

在数据量很大的时候，使用快排，取 pivot 时，进行优化，例如随机，3 数取中。

在序列元素很少时，使用插入排序，例如当递归到只有 4 个元素时，快排算法需要 12 次，而插入排序最多只需要 16 次，如果序列的有序度不那么差，插入排序会比快排性能要好。

EOF