线性排序

简述

1. 桶排序（借助快排）
2. 计数排序（借助数组下标）
3. 基数排序（借鉴“稳定排序”思路）

共同点：

算法复杂度：$O(n)$

对数据要求苛刻。

桶排序

解释：

假设要按照 100w 用户的年龄进行排序。年龄设置最大 120 岁。设置 12 个桶，第一个桶里，放 0-10岁的用户，第二个桶里，放 11 -20岁的用户，依次类推。

遍历所有数据，将用户按照年龄放到对应的桶里。然后对每个桶，进行快速排序。

复杂度：

假设有 n 个数据，m 个桶，每个桶里是 k 个数据。

那么每个桶的复杂度就是 k * logk。所有桶的复杂度就是 m * k * logk。

因为 k = n/m，代入之后，n/m * m * logk = n * logk。

如果 m 接近 n，那么 k 的值就会很小，那么 logk 也就很小，所以他时间复杂度是 $O(n)$.

关键字：有序桶，快排。

计数排序

计数排序是桶排序的一种特殊情况。

假设：现在，我们要给 120 个学生的分数进行排序，分数是 0 - 100；如何在 $O(n)$ 的时间复杂度里，实现按照分数排序？

我们可以设计一个长度为 101 的数组，数组下标对应 0-100 分值，数组内容记录每个分值的人数即可。

计数排序的 “计数” 的意思是，记住每个槽位记录的是重复值的数量。

基数排序

如下图，有 5 行数据，每个数据由 3 个字母组成，我们可以认为是电话号码。

我们第一次比较这 5 行数据的最后一位，并对他们整体进行排序。

第二次比较这 5 行数据的第二位，并对他们 整体进行排序。

第三次比较这 5行数据的第一位，并对他们整体进行排序。

注意：基数排序，每次排序必须都是稳定的，如果不是稳定的，那么上次的排序将失去价值。

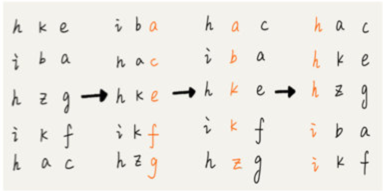
基数排序对要排序的数据是有要求的，需要可以分割出独立的“位”来比较，而且位之间有递进的关系，如果 a 数据的高位比 b 数据大，那剩下的低位就不用比较了。除此之外，每一位的数据范围不能太大，要可以用线性排序算法来排序，否则，基数排序的时间复杂度就无法做到 $O(n)$ 了;