归并排序

分治是一种思路。

递归是一种技巧。

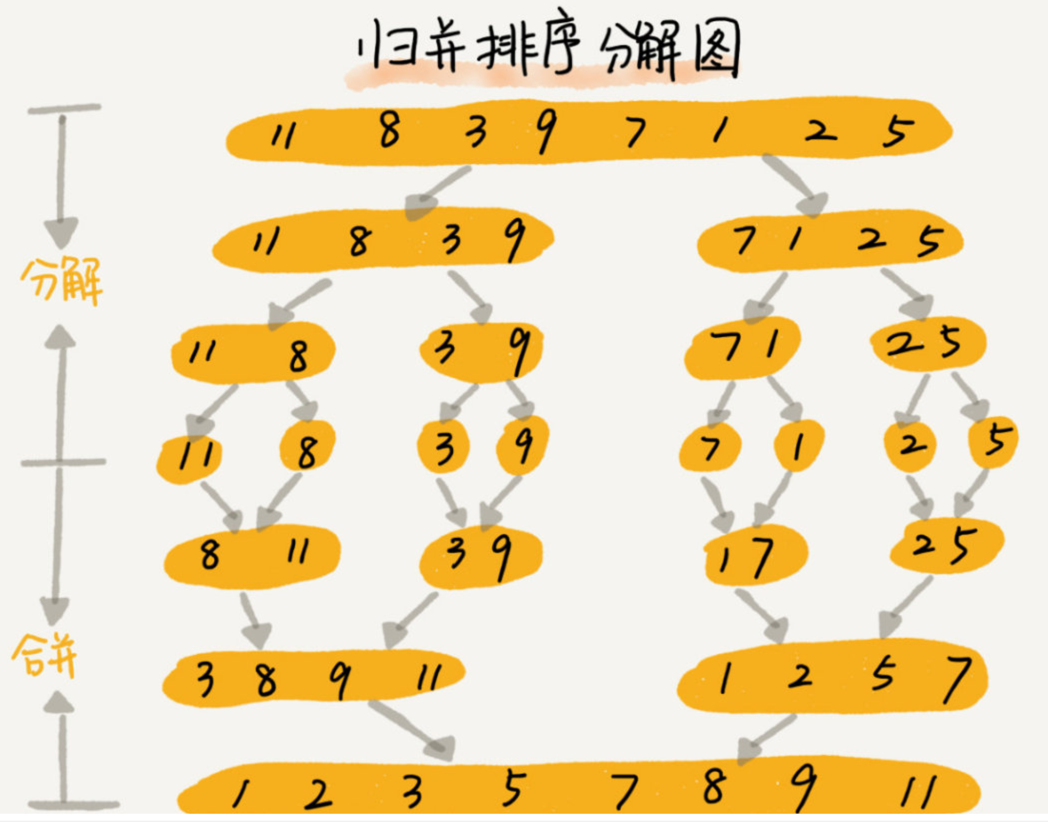
分治算法的思想：将原问题分解为几个规模较小但类似于原问题的子问题，递归的求解这些子问题，然后再合并这些子问题的解来建立原问题的解。

分治模式在每层递归时都有 3 个步骤：

1. 分解，分解原问题为子问题。这些子问题是原问题的规模较小的实例。
2. 解决，递归的求解子问题。
3. 合并。合并子问题的解为原问题的解。

归并排序

归并排序完全遵循分治思想。操作如下：

1. 分解：分解待排序的 n 个元素，序列成剧透 2/n 个元素的 2 个子序列。
2. 解决，使用归并排序，递归的排序 2 个子序列。
3. 合并，合并两个子序列以产生已排序的答案。

当待排序的序列长度为 1 时，递归开始“回升”，在这种情况下，不要做任何工作，因为长度为 1 的序列已经排好序了。

归并排序的关键 步骤，在于“合并”。

通常这个合并函数，叫做 merge。他的职责就是将 2 个有序的序列，合并成一个有序的序列。

如果是你，你怎么合并呢？

思路：假设，现在有 1 个数组，被分成了 2 个有序的序列。我们可以新申请一个临时数组，将数据从最小的下标开始，依次比较，谁小，谁就放入到 临时 数组中，然后下次，下标递增，继续比较。

具体过程如下图：

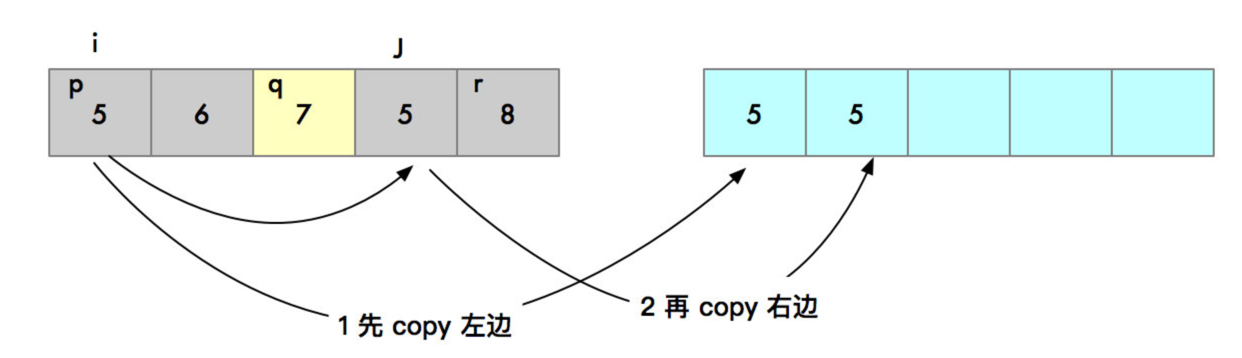
代码如下：

public class 归并排序 {
    public static void main(String[] args) {
        int[] arr = {5, 1, 11, 2, 0, 6, 9, 4 };
        sort(arr, 0, arr.length - 1);
        System.out.println(Arrays.toString(arr));
    }

    private static int[] sort(int[] arr, int start, int end) {
        if (start >= end) {
            return arr;
        }
				// 防止溢出
        int mid = start + (end - start) / 2;

        sort(arr, start, mid);
        sort(arr, mid + 1, end);

        return merge(arr, start, mid, end);
    }

    private static int[] merge(int[] arr, int p, int q, int r) {
        int i = p;
        // 这里必须 + 1, 以 q 作为分割点.
        int j = q + 1;
        int tmpIndex = 0;

        int[] tmp = new int[r - i + 1];

        while (i <= q && j <= r) {
          	// 保证排序算法稳定性
            if (arr[i] <= arr[j]) {
                tmp[tmpIndex++] = arr[i++];
            } else {
                tmp[tmpIndex++] = arr[j++];
            }
        }

        int start = i;
        int end = q;

        if (j < r) {
            start = j;
            end = r;
        }

        for (int k = start; k <= end; k++) {
            tmp[tmpIndex++] = arr[k];
        }

        for (int k = 0; k < tmpIndex; k++) {
            arr[p++] = tmp[k];
        }

        return arr;
    }
}

代码中，有 2 个函数：

$sort(int [] arr, int start, int end)$

$merge(int [] arr, int p, int q, int r)$

sort 函数用来分割数组，终止条件为，直到分割成只有一个元素（只有一个元素的序列，是不用排序的）。

merge 函数用来合并数组，例如，在递归树的最下层，一定是从 【0， 1】开始合并的，merge 函数会合并这两个下标的元素，变成有序的序列。

merge 函数的流程：

1. 创建 i j 下标 和 tmp 数组。
2. 循环原数组，将 i 和 j 递增进行比较，并进行比较，然后把较小的值，依次放入到 tmp 数组中。
3. 如果 i 或者 j 比较结束，就需要将未比较结束的，copy 到 tmp 数组中。
4. 最后，将 tmp 数组的数据，copy 到原数组中。

这样就完成了 归并排序 中，最为关键的合并。

从上面的代码中，也可以看到，最为核心的代码，就是 merge 函数。

排序算法 三 问

1 是原地排序吗

答案，不是原地排序的。

在 merge 函数中，我们需要申请一个临时数组，将两个区间的元素逐个 copy 进临时数组中，这就不是原地的了。而 归并排序的空间复杂度，也因此比“原地排序” 的算法，要高。

多高呢？由于归并排序使用递归计算，每次只有一个函数在执行，同一时刻，只会申请一个临时数组，因此，如果申请的 大小 为 n 的数组，那么他的空间复杂度就是 $O(n)$.

2 是稳定的吗

答案是稳定的（只要你实现的正确）。

假设两个数组中，有相同的两个元素，例如：

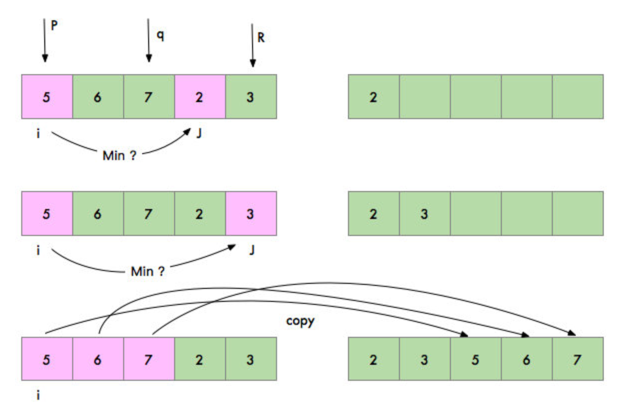
上图中， i 和 j 的位置，元素都是5， 遇到这种情况，在算法中，我们可以先将左边的那个 5 拷贝到 tmp 数组中，然后再下次比较时，再将 右边的那个 5 ，拷贝到 tmp 数组中。

代码怎么写呢？

if （arr[i] <= arr[j]）{
		tmp[index++] = arr[i++];
} else if(arr[j] < arr[i]){
    tmp[index++] = arr[j++];
}

可以看到，在 i 和 j 元素的比较中，$=$ 等于号，必不可少。如果没有等于号，那么，他将不是稳定的。

3 三种时间复杂度是多少

实质上，对归并排序的时间复杂度分析，就是对“分治算法’’ 的时间复杂度分析。

在《算法导论》 2.3.2 中，作者 告诉我们如何分析分治算法。

当一个算法包含对其自身的递归调用时，我们往往可以用递归方程或递归式来描述其 运行时间。

递归方程 或 递归式。

递归式：

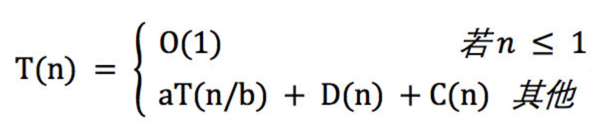
分治算法运行时间的递归式，来自其基本模式的三个步骤。

通过推演，我们可以知道，归并算法的时间复杂度 $O(nlogn)$ ，具体推演参见《递归时间复杂度 递归树 推演计算》。

另外，归并排序的时间复杂度，和原始数组是否有序没有关系，算法的最好，最坏，平均，时间复杂度都是 $O(nlogn)$ 。是一个非常稳定的排序算法。

总结

归并排序，

分治算法。

非原地排序，空间复杂度 $O(n)$。

稳定性好。

所有情况下复杂度都为 $O(nlogn)$ ，

merge 函数为核心逻辑，临时数组 i j 拷贝。

EOF